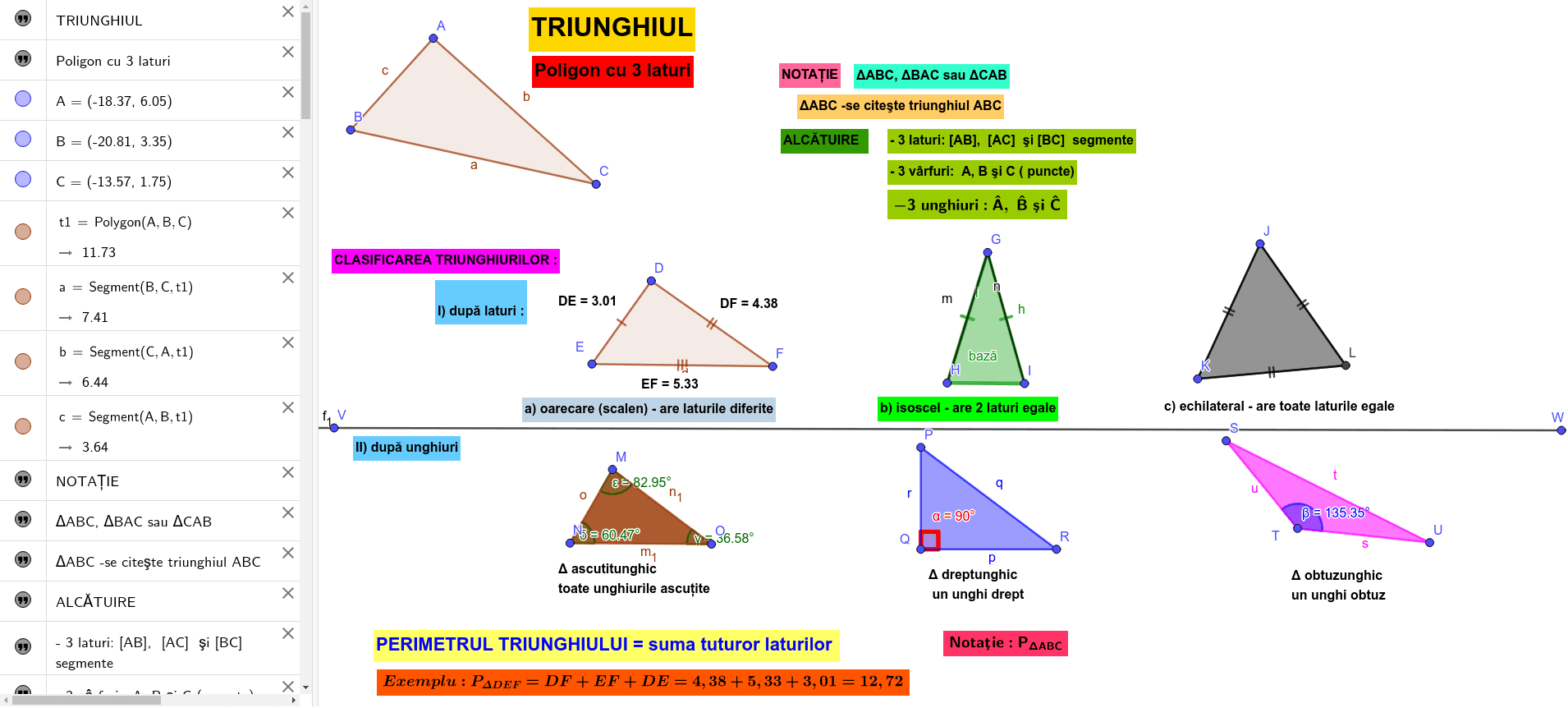
Triunghiul. Perimetrul triunghului. Tipuri de triunghiuri în funcție de unghiuri
Triunghiurile sunt figuri geometrice fundamentale în matematică și în multe aspecte ale științei și ingineriei. Unul dintre conceptele de bază în studierea triunghiurilor este perimetrul său, care reprezintă suma lungimilor laturilor sale. În plus, triunghiurile pot fi clasificate în funcție de măsurile unghiurilor lor, ceea ce ne permite să înțelegem mai bine proprietățile lor geometrice și relațiile dintre laturi și unghiuri.
Perimetrul Triunghiului:
Perimetrul unui triunghi este suma lungimilor laturilor sale. Pentru un triunghi cu laturile de lungimi a, b și c, perimetrul P poate fi calculat folosind formula:
[ P = a + b + c ]
Această sumă a lungimilor laturilor este esențială în calcularea și compararea dimensiunilor geometrice ale triunghiurilor.
Tipuri de Triunghiuri în Funcție de Unghiuri:
Triunghiurile pot fi clasificate în funcție de măsurile unghiurilor lor. Există trei tipuri principale de triunghiuri în acest sens: triunghiurile acute, triunghiurile obtuze și triunghiurile dreptunghice.
- Triunghiurile acute:
Triunghiurile acute sunt acelea în care toate unghiurile sunt mai mici de 90 de grade. În acest tip de triunghi, toate laturile sunt mai mici decât diagonala sa, iar suma unghiurilor interioare este întotdeauna mai mică de 180 de grade. - Triunghiurile obtuze:
Triunghiurile obtuze sunt acelea în care unul dintre unghiuri este mai mare de 90 de grade. În acest caz, latura opusă unghiului obtuz este cea mai lungă dintre cele trei, iar suma unghiurilor interioare este totdeauna mai mică de 180 de grade. - Triunghiurile dreptunghice:
Triunghiurile dreptunghice sunt acelea în care unul dintre unghiuri este un unghi drept, adică are 90 de grade. Acest tip de triunghi este deosebit de interesant din punct de vedere geometric deoarece respectă teorema lui Pitagora, conform căreia suma pătratelor lungimilor catetelor este egală cu pătratul lungimii ipotenuzei. - Perimetrul unui triunghi este o măsură fundamentală a dimensiunilor sale geometrice, iar clasificarea triunghiurilor în funcție de unghiurile lor ne ajută să înțelegem mai bine proprietățile lor și relațiile dintre laturi și unghiuri. Această înțelegere este esențială în matematică și în domenii precum fizica, ingineria și designul.
 07.02.2024
07.02.2024