CEDRA

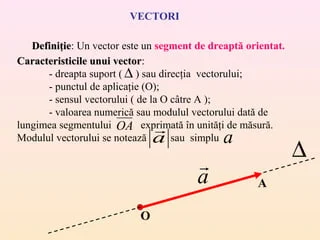
Segment orientat

Un segment orientat este o noțiune geometrică care presupune un segment de dreaptă ce are o direcție specificată. Într-un segment orientat, pe lângă cele două extremități (capete), se specifică un sens de parcurs, de la un capăt la celălalt. Dacă notăm segmentul cu extremitățile ( A ) și ( B ), segmentul orientat de la ( A ) la ( B ) se notează ( \overrightarrow{AB} ). Segmentul orientat este important în studiul vectorilor, deoarece direcția și sensul segmentului sunt folosite pentru a defini vectorii.

Vectori

Un vector este un obiect matematic ce reprezintă o mărime cu atât o magnitudine (lungime) cât și o direcție. Vectorii sunt esențiali în multe domenii ale matematicii, fizicii și ingineriei, fiind folosiți pentru a modela forțe, deplasări și alte concepte care necesită descrierea unei direcții și a unei magnitudini. Un vector poate fi reprezentat grafic printr-un segment orientat, unde lungimea segmentului reprezintă magnitudinea vectorului și direcția segmentului reprezintă direcția vectorului. De exemplu, vectorul ( \overrightarrow{AB} ) are punctul de început ( A ) și punctul de sfârșit ( B ), iar lungimea sa este distanța dintre ( A ) și ( B ).

Vectori coliniari

Vectorii coliniari sunt vectori care se află pe aceeași dreaptă sau pe drepte paralele. Acest lucru înseamnă că vectorii au aceeași direcție sau direcții opuse. Dacă doi vectori sunt coliniari, atunci unul poate fi exprimat ca o scalară a celuilalt. Matematic, vectorii ( \mathbf{u} ) și ( \mathbf{v} ) sunt coliniari dacă există un număr real ( k ) astfel încât ( \mathbf{u} = k \mathbf{v} ). De exemplu, vectorii ( \overrightarrow{AB} ) și ( \overrightarrow{CD} ) sunt coliniari dacă și numai dacă există un scalar ( k ) astfel încât ( \overrightarrow{AB} = k \overrightarrow{CD} ). În contextul fizic și geometric, coliniaritatea vectorilor poate simplifica multe calcule și analize, deoarece proprietățile coliniarității permit reducerea complexității problemei la o singură dimensiune.