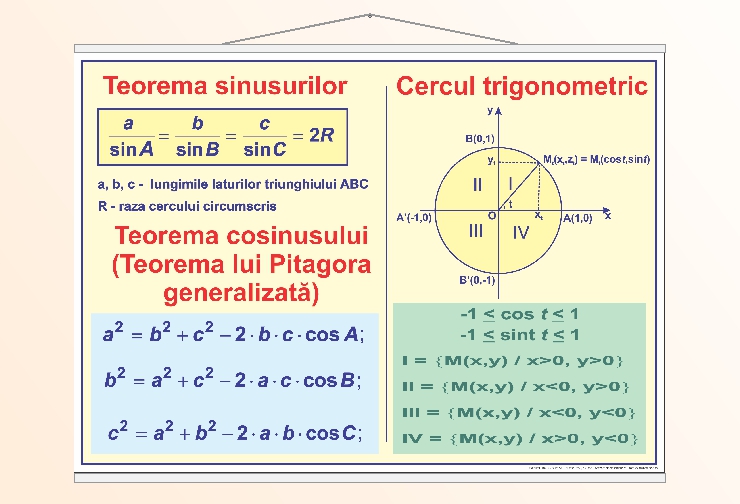
Teorema sinusurilor şi teorema cosinusului
Calculul lungimii unui segment și a măsurii unui unghi în geometrie se realizează adesea folosind teorema sinusurilor și teorema cosinusului, două instrumente fundamentale în trigonometrie. Aceste teoreme sunt esențiale pentru rezolvarea triunghiurilor, fie ele dreptunghice sau oblice.
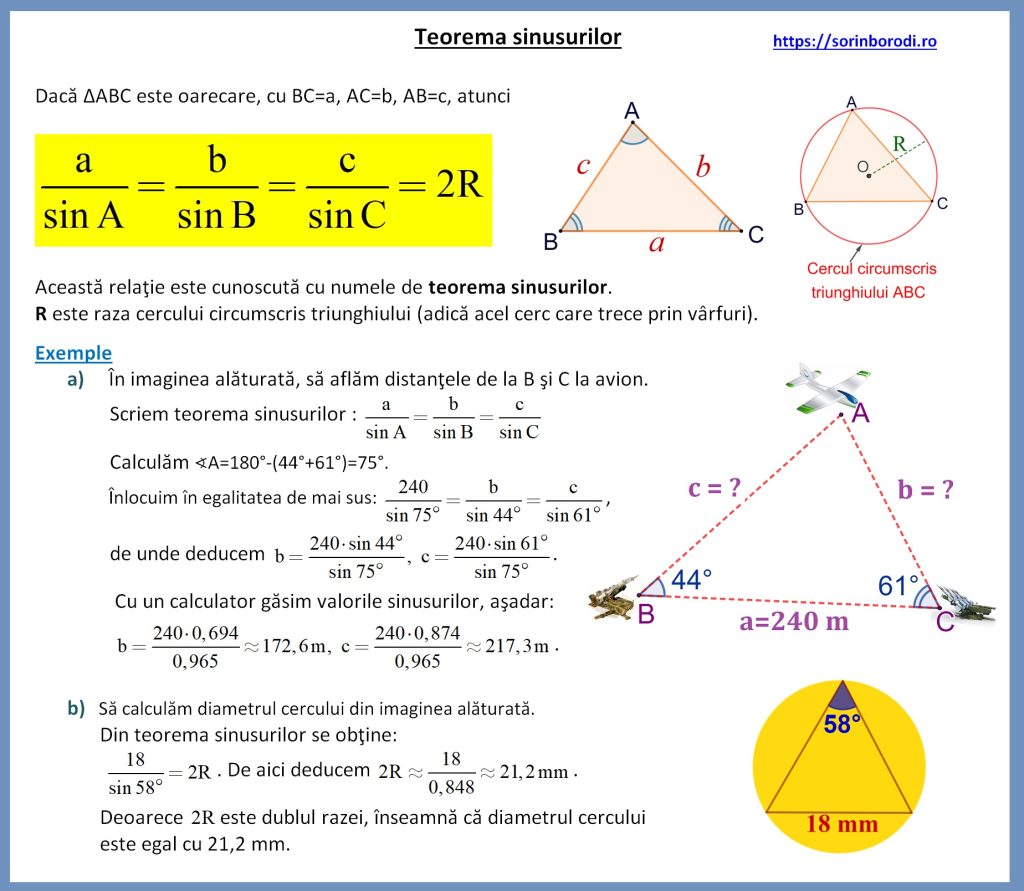
Teorema sinusurilor
Teorema sinusurilor afirmă că, într-un triunghi, raportul dintre lungimea unei laturi și sinusul unghiului opus este constant pentru toate cele trei laturi și unghiuri ale triunghiului. Matematic, aceasta este exprimată astfel:
[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R] unde (a), (b) și (c) sunt lungimile laturilor triunghiului, (A), (B) și (C) sunt măsurile unghiurilor opuse acestor laturi, iar (R) este raza cercului circumscris triunghiului. Această teoremă este utilă pentru determinarea lungimilor laturilor necunoscute sau a măsurilor unghiurilor într-un triunghi, atunci când sunt cunoscute suficiente date inițiale.
Teorema cosinusului
Teorema cosinusului, cunoscută și ca teorema lui Pitagora generalizată, este utilizată pentru a calcula lungimea unei laturi a unui triunghi atunci când sunt cunoscute lungimile celorlalte două laturi și măsura unghiului dintre ele. Aceasta se exprimă prin:
[ c^2 = a^2 + b^2 – 2ab \cos C ], unde (a) și (b) sunt lungimile celor două laturi cunoscute, (C) este unghiul dintre aceste laturi, iar (c) este lungimea laturii opuse unghiului (C). Teorema cosinusului este deosebit de utilă în triunghiurile oblice, unde unghiurile nu sunt neapărat de 90 de grade.
Prin utilizarea teoremei sinusurilor și a teoremei cosinusului, se pot rezolva probleme complexe de geometrie plană. Aceste teoreme oferă metode precise pentru determinarea lungimilor și unghiurilor necunoscute, facilitând astfel înțelegerea și aplicarea conceptelor geometrice în diverse domenii, de la arhitectură și inginerie până la astronomie și fizică.
 01.07.2024
01.07.2024