
Compunerea funcţiilor, exemple pe funcţii numerice
Compunerea funcțiilor este un concept fundamental în matematică, cu aplicații extinse în diverse domenii precum analiza matematică, fizica și informatica. Procesul de compunere a funcțiilor implică utilizarea rezultatelor unei funcții ca intrări pentru o altă funcție. Dacă avem două funcții ( f: X \rightarrow Y ) și ( g: Y \rightarrow Z ), compunerea funcțiilor ( f ) și ( g ) este o nouă funcție ( h: X \rightarrow Z ) definită prin ( h(x) = g(f(x)) ) pentru toate ( x ) în domeniul de definiție al lui ( f ).
Exemple pe funcții numerice
Exemplul 1:
Să considerăm două funcții numerice simple:
[ f(x) = 2x + 3 ]
[ g(x) = x^2 ]
Pentru a compune aceste funcții, calculăm mai întâi ( f(x) ) și apoi aplicăm ( g ) asupra rezultatului obținut:
[ (g \circ f)(x) = g(f(x)) = g(2x + 3) ]
[ g(2x + 3) = (2x + 3)^2 ]
Astfel, funcția compusă ( h(x) = g(f(x)) ) devine:
[ h(x) = (2x + 3)^2 ]
Exemplul 2:
Să considerăm alte două funcții numerice:
[ f(x) = \sin(x) ]
[ g(x) = e^x ]
Compunerea acestor funcții se face aplicând mai întâi funcția ( f ) și apoi funcția ( g ):
[ (g \circ f)(x) = g(f(x)) = g(\sin(x)) ]
[ g(\sin(x)) = e^{\sin(x)} ]
Prin urmare, funcția compusă ( h(x) = g(f(x)) ) devine:
[ h(x) = e^{\sin(x)} ]
Proprietăți și observații
Compunerea funcțiilor este asociativă, dar nu este comutativă. Asociativitatea implică faptul că pentru orice trei funcții ( f ), ( g ) și ( h ), avem:
[ (h \circ (g \circ f)) = ((h \circ g) \circ f) ]
Lipsa comutativității se poate observa ușor: în general, ( g(f(x)) \neq f(g(x)) ). De exemplu, folosind funcțiile din primul exemplu:
[ (f \circ g)(x) = f(g(x)) = f(x^2) = 2x^2 + 3 ]
care este diferit de ( g(f(x)) = (2x + 3)^2 ).
Compunerea funcțiilor este un instrument puternic în matematică, permițând combinarea unor funcții simple pentru a crea funcții mai complexe. Acest proces este esențial pentru modelarea și soluționarea problemelor în multe ramuri ale științei și tehnologiei.
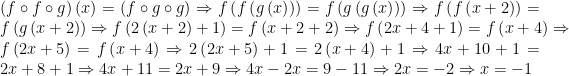
 12.04.2024
12.04.2024