CEDRA

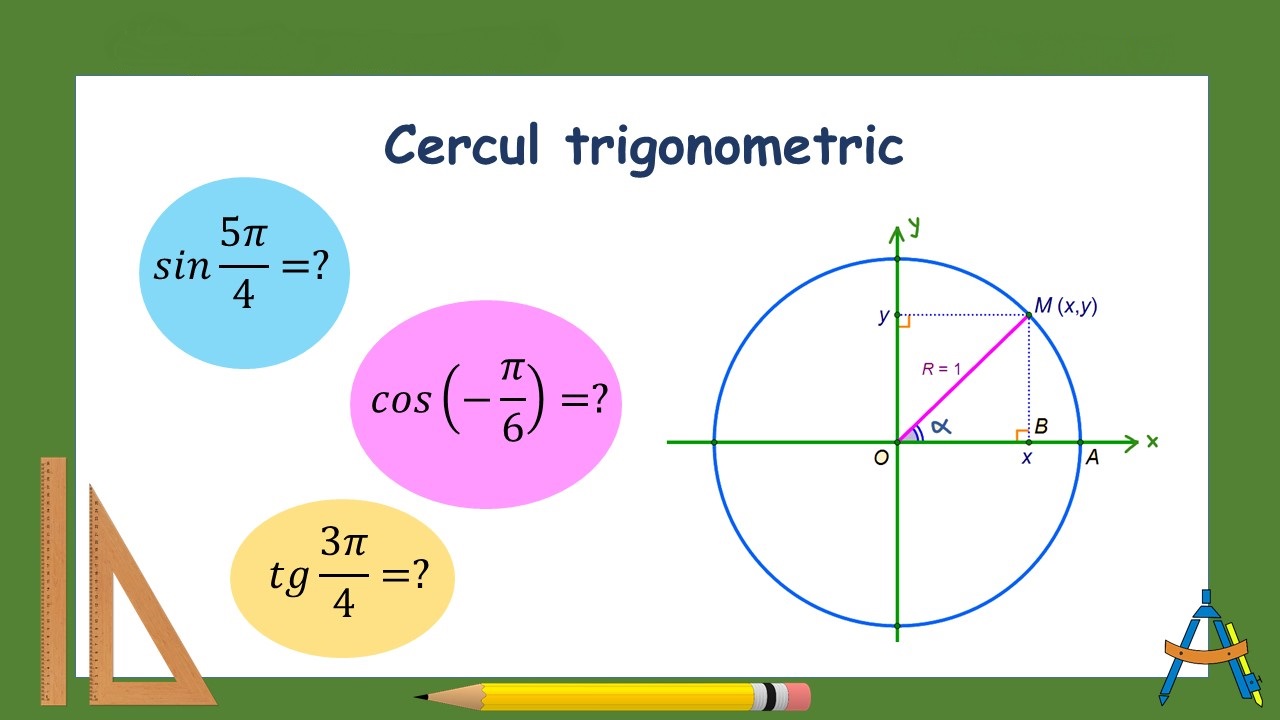
Cercul trigonometric reprezintă un instrument esențial în studiul trigonometriei, oferind o metodă vizuală și geometrică pentru definirea și înțelegerea funcțiilor trigonometrice. Cercul trigonometric este un cerc cu raza unitară (raza egală cu 1) plasat într-un sistem de coordonate cartezian, având centrul în origine (punctul (0, 0)). Pe acest cerc, fiecare unghi poate fi reprezentat printr-un punct corespunzător pe circumferința cercului, ceea ce permite determinarea valorilor funcțiilor trigonometrice.

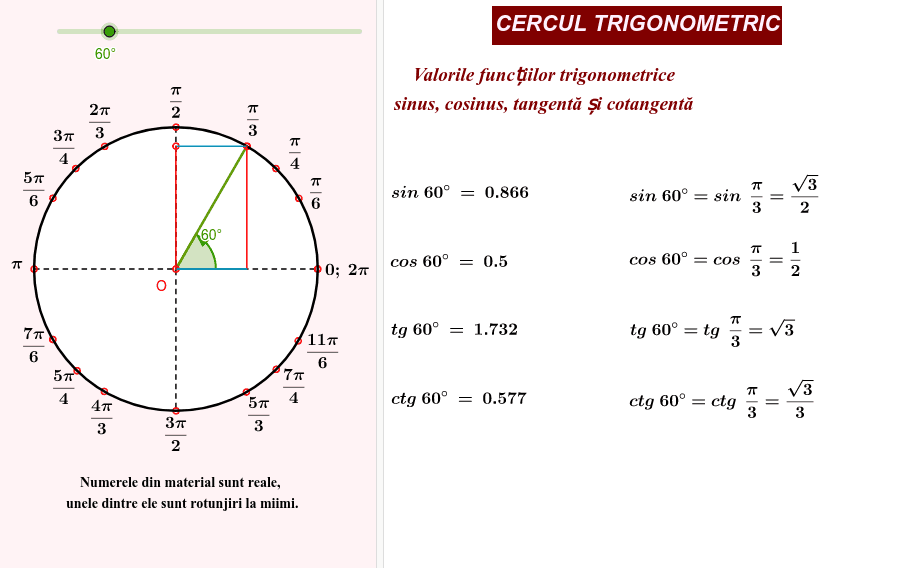
Funcțiile trigonometrice fundamentale, sin (sinus), cos (cosinus) și tan (tangenta), sunt definite pe baza coordonatelor punctelor de pe cercul trigonometric. Pentru un unghi (\theta), sinusul acestuia (sin((\theta))) reprezintă coordonata y a punctului de pe cercul trigonometric asociat cu unghiul respectiv, iar cosinusul (cos((\theta))) reprezintă coordonata x. Aceste relații se pot vizualiza clar pe cercul trigonometric, unde sin((\theta)) este proiecția punctului pe axa verticală, iar cos((\theta)) este proiecția punctului pe axa orizontală.

Tangenta (tan((\theta))) este definită ca raportul dintre sinus și cosinus, adică tan((\theta)) = sin((\theta))/cos((\theta)). În contextul cercului trigonometric, tangenta unghiului (\theta) poate fi vizualizată ca lungimea segmentului de dreaptă care atinge cercul la punctul unde unghiul (\theta) intersectează axa tangentei. Această definiție ajută la înțelegerea periodicității și simetriei funcțiilor trigonometrice, esențiale în diverse aplicații matematice și fizice.

Utilizarea cercului trigonometric facilitează înțelegerea identităților trigonometrice și a proprietăților acestor funcții, cum ar fi periodicitatea, simetria și relațiile reciproce. De exemplu, identitățile fundamentale cum ar fi sin^2((\theta)) + cos^2((\theta)) = 1 și relațiile de cofuncție (sin((\pi/2 – (\theta))) = cos((\theta)) și cos((\pi/2 – (\theta))) = sin((\theta))) pot fi demonstrate ușor folosind cercul trigonometric.

În concluzie, cercul trigonometric reprezintă un concept fundamental și o unealtă vizuală indispensabilă pentru definirea și înțelegerea funcțiilor trigonometrice. Prin utilizarea sa, studenții și matematicienii pot explora și demonstra proprietățile acestor funcții, facilitând aplicarea lor în probleme diverse din matematică, fizică și inginerie.