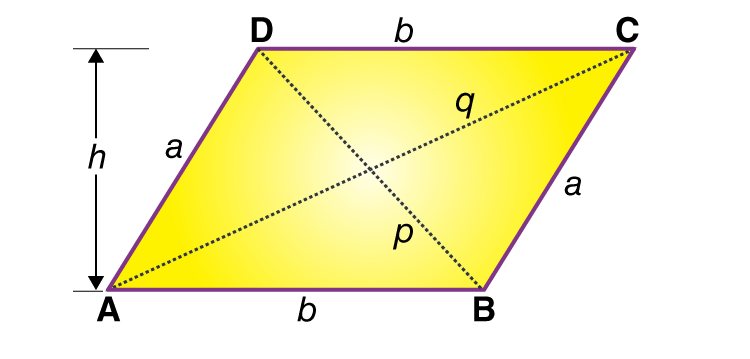
Paralelogramul – o figura geometrică fundamentală
Proprietăţi ale paralelogramului
Paralelogramul este o figură geometrică cu patru laturi, în care fiecare pereche de laturi opuse este paralelă și de lungime egală. Printre principalele proprietăţi ale paralelogramului se numără:
- Laturile opuse sunt paralele și congruente: Aceasta înseamnă că laturile opuse ale paralelogramului sunt egale ca lungime și paralele între ele.
- Unghiurile opuse sunt congruente: Într-un paralelogram, unghiurile opuse sunt egale.
- Diagonalele se înjumătățesc reciproc: Diagonalele unui paralelogram se intersectează în punctul de mijloc și se înjumătățesc reciproc.
- Suma unghiurilor adiacente este de 180 de grade: Două unghiuri adiacente într-un paralelogram sunt suplementare, adică suma lor este de 180 de grade.
Aplicaţii ale paralelogramului în geometria triunghiului
Paralelogramul are multiple aplicații în geometria triunghiului, două dintre cele mai importante fiind utilizarea sa în definirea liniei mijlocii și în determinarea centrului de greutate al unui triunghi.
Linia mijlocie în triunghi
Linia mijlocie a unui triunghi este segmentul care unește mijloacele a două laturi ale triunghiului. O proprietate importantă a acestei linii este că ea este paralelă cu a treia latură și are jumătate din lungimea acesteia.
Pentru a demonstra această proprietate, putem utiliza un paralelogram. Dacă desenăm linia mijlocie și o paralelăm cu a treia latură, formăm un paralelogram în care linia mijlocie și a treia latură sunt laturi opuse. Astfel, datorită proprietății de paralelism și lungime egală a laturilor opuse într-un paralelogram, linia mijlocie va fi paralelă și va avea jumătate din lungimea laturii corespunzătoare a triunghiului.
Centrul de greutate al unui triunghi
Centrul de greutate (sau centroidul) al unui triunghi este punctul de intersecție al medianelor triunghiului. Medianele sunt segmentele care unesc vârfurile triunghiului cu mijloacele laturilor opuse. Proprietatea fundamentală a centrului de greutate este că el împarte fiecare mediană în raportul 2:1, măsurat de la vârf către mijlocul laturii.
Această proprietate poate fi demonstrată prin utilizarea paralelogramelor. Dacă desenăm medianele și considerăm paralelograma formată de aceste segmente, putem vedea că fiecare mediană este o diagonală a unui paralelogram care este înjumătățită în punctul de intersecție. Astfel, centrul de greutate al triunghiului poate fi interpretat ca punctul de intersecție al diagonalelor unui paralelogram, demonstrând astfel că acesta împarte medianele în raportul specificat.
Paralelogramul nu este doar o figură geometrică de bază, ci și un instrument esențial în studiul geometriei triunghiului, oferind soluții și demonstrații pentru probleme importante, precum linia mijlocie și centrul de greutate al unui triunghi.
 08.05.2024
08.05.2024