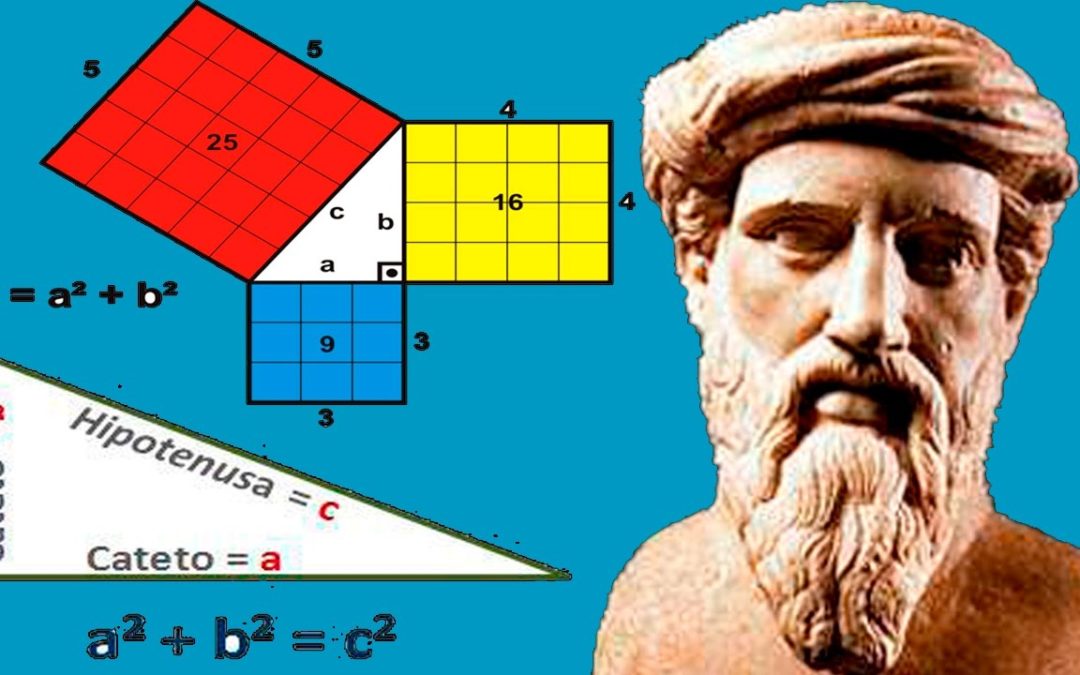
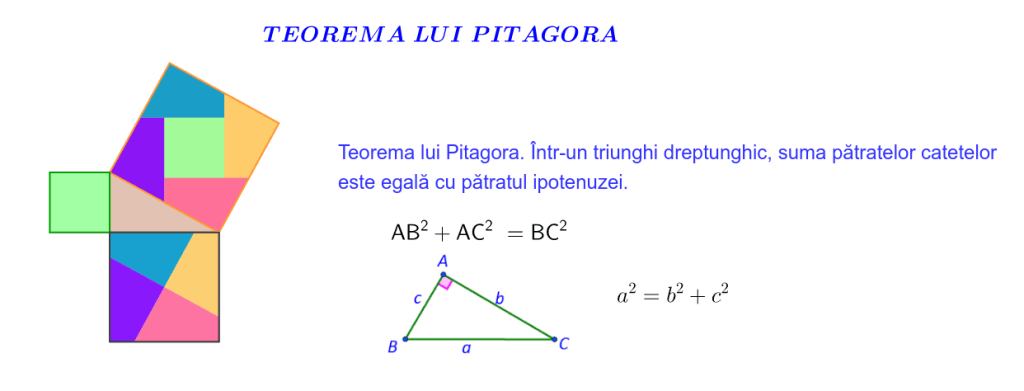
Teorema lui Pitagora este una dintre cele mai cunoscute și importante teoreme din geometrie. Ea descrie o relație fundamentală între laturile unui triunghi dreptunghic.

Enunțul teoremei

În orice triunghi dreptunghic, pătratul lungimii ipotenuzei este egal cu suma pătratelor lungimilor catetelor.

Matematic, dacă triunghiul dreptunghic are catetele aaa și bbb, iar ipotenuza este ccc, atunci teorema se scrie astfel: c2=a2+b2c^2 = a^2 + b^2c2=a2+b2

Explicație

• Catetele sunt laturile care formează unghiul drept (90°).
• Ipotenuza este latura opusă unghiului drept și este cea mai lungă latură a triunghiului dreptunghic.

Această relație permite calcularea lungimii unei laturi necunoscute atunci când se cunosc celelalte două laturi.

Exemple de aplicare

1. Calcularea ipotenuzei:
   Dacă un triunghi dreptunghic are catetele de 3 cm și 4 cm, lungimea ipotenuzei se calculează astfel: c2=32+42=9+16=25  ⟹  c=5 cmc^2 = 3^2 + 4^2 = 9 + 16 = 25 \implies c = 5 \text{ cm}c2=32+42=9+16=25⟹c=5 cm
2. Calcularea unei catete:
   Dacă ipotenuza este de 13 cm, iar o catetă de 5 cm, cealaltă catetă se află astfel: b2=c2−a2=132−52=169−25=144  ⟹  b=12 cmb^2 = c^2 – a^2 = 13^2 – 5^2 = 169 – 25 = 144 \implies b = 12 \text{ cm}b2=c2−a2=132−52=169−25=144⟹b=12 cm

Utilizări

Teorema lui Pitagora este folosită frecvent în:

• Geometrie și trigonometrie;
• Construcții și arhitectură;
• Fizică și inginerie, pentru calculul distanțelor;
• Viața de zi cu zi, de exemplu, în determinarea diagonalei unui dreptunghi.

Curiozitate istorică

Teorema îi poartă numele celebrului matematician grec Pitagora, care a trăit în secolul al VI-lea î.Hr. Totuși, dovezi arată că civilizații mult mai vechi, precum egiptenii și babilonienii, cunoșteau această relație și o foloseau practic.

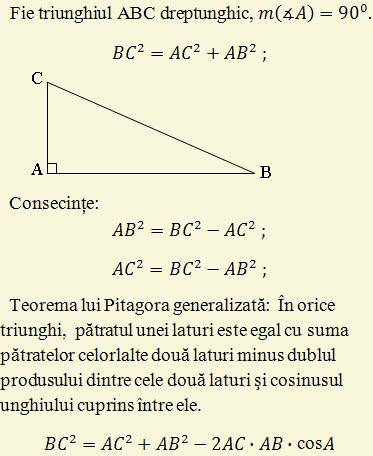
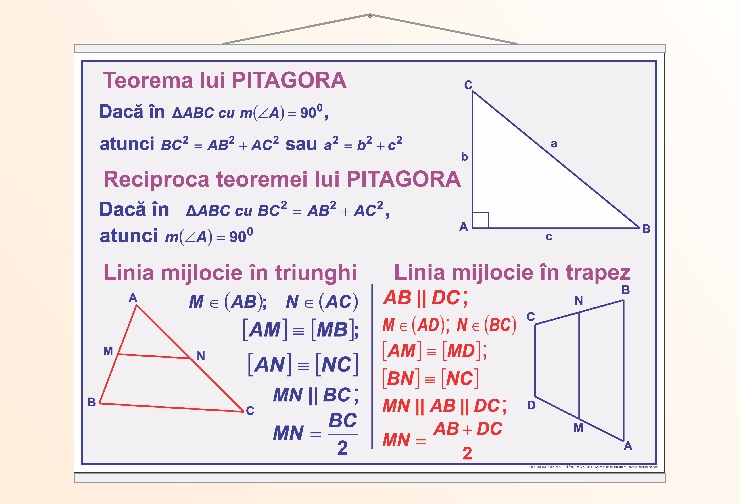
Fișă de lucru – Teorema lui Pitagora

1. Teorema lui Pitagora

Enunț: În orice triunghi dreptunghic, pătratul lungimii ipotenuzei este egal cu suma pătratelor lungimilor catetelor. c2=a2+b2c^2 = a^2 + b^2c2=a2+b2

• aaa și bbb – catetele (laturile care formează unghiul drept)
• ccc – ipotenuza (latura opusă unghiului drept)

Sugestie de desen: Triunghi dreptunghic cu pătratele construite pe fiecare latură.

2. Exemple explicative

Exemplul 1 – Calculul ipotenuzei

• Catetele: a=3 cm,b=4 cma = 3 \text{ cm}, b = 4 \text{ cm}a=3 cm,b=4 cm

c2=32+42=9+16=25  ⟹  c=5 cmc^2 = 3^2 + 4^2 = 9 + 16 = 25 \implies c = 5 \text{ cm}c2=32+42=9+16=25⟹c=5 cm

Exemplul 2 – Calculul unei catete

• Ipotenuza: c=13 cmc = 13 \text{ cm}c=13 cm
• Catetă cunoscută: a=5 cma = 5 \text{ cm}a=5 cm

b2=c2−a2=169−25=144  ⟹  b=12 cmb^2 = c^2 – a^2 = 169 – 25 = 144 \implies b = 12 \text{ cm}b2=c2−a2=169−25=144⟹b=12 cm

3. Exerciții pentru elevi

Exercițiul 1
Triunghi dreptunghic cu catetele a=6 cma = 6 \text{ cm}a=6 cm și b=8 cmb = 8 \text{ cm}b=8 cm.
Calculați lungimea ipotenuzei ccc.

Exercițiul 2
Triunghi dreptunghic cu ipotenuza c=10 cmc = 10 \text{ cm}c=10 cm și o catetă a=6 cma = 6 \text{ cm}a=6 cm.
Calculați cealaltă catetă bbb.

Exercițiul 3 – Problema practică
O scară se sprijină de peretele unei case astfel încât baza scării este la 3 m de perete, iar scara ajunge la o înălțime de 4 m pe perete.

• Care este lungimea scării?

4. Aplicări practice

• Determinarea diagonalelor în dreptunghiuri sau pătrate.
• Construcții și amenajări (rampe, scări).
• Fizică și inginerie: calculul distanțelor și traiectoriilor.
• Viața cotidiană: măsurarea unor spații inaccesibile direct.

5. Curiozitate istorică

Teorema poartă numele lui Pitagora, matematician grec din secolul VI î.Hr., însă civizații egiptene și babiloniene foloseau această relație cu sute de ani înainte pentru construcții și măsurători practice.