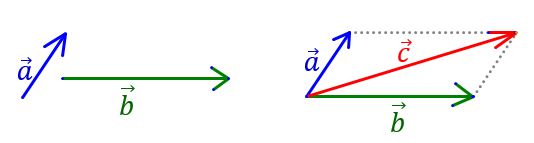
Vectorii. Mărimi vectoriale
În viața de zi cu zi și în fizică întâlnim mărimi care nu pot fi descrise complet doar printr-un număr. Acestea se numesc mărimi vectoriale. Spre deosebire de mărimile scalare, care au doar valoare numerică și unitate de măsură (cum ar fi masa sau temperatura), mărimile vectoriale au valoare, direcție și sens. Exemple de mărimi vectoriale sunt viteza, forța, deplasarea, accelerația sau momentul de forță.
Un vector este o reprezentare matematică a unei mărimi vectoriale. El este adesea ilustrat printr-o săgeată:
- lungimea săgeții indică valoarea mărimii;
- orientarea săgeții arată direcția mărimii;
- capul săgeții indică sensul în care acționează mărimea.
Elementele unui vector
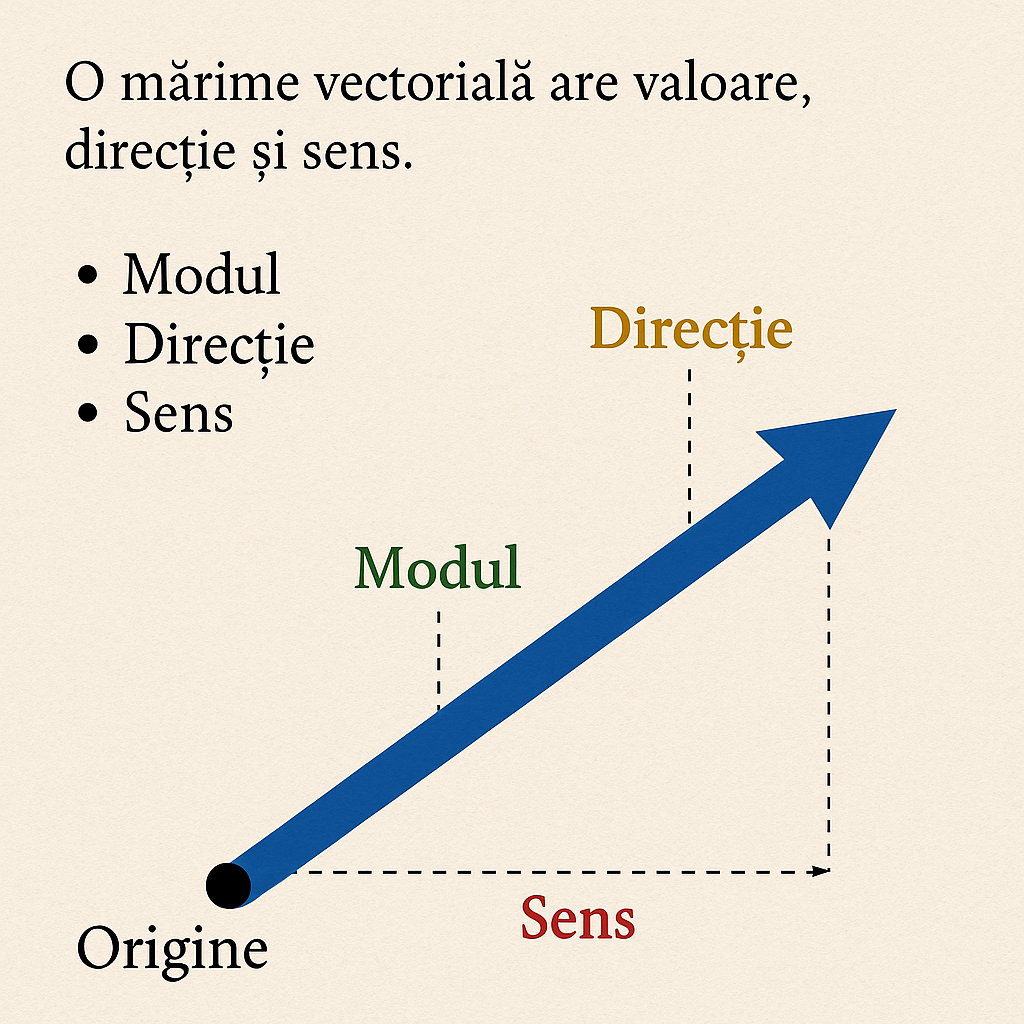
Fiecare vector are trei caracteristici principale:
- Modulul (mărimea vectorului) – exprimă cât de mare este mărimea;
- Direcția – linia pe care se află vectorul în spațiu;
- Sensul – orientarea vectorului de-a lungul direcției.
De exemplu, dacă tragem o cutie cu o forță de 50 N spre nord, vectorul forței are modulul 50 N, direcția spre nord și sensul înspre locul în care tragem cutia.
Reprezentarea vectorilor
Vectorii pot fi reprezentați în mai multe moduri:
- Grafic – printr-o săgeată desenată pe hârtie;
- Analitic – folosind coordonate în sistemul de axe (x, y, z), de exemplu: A⃗=(3,4)\vec{A} = (3, 4)A=(3,4);
- Notational – prin litere cu săgeată deasupra: v⃗\vec{v}v, F⃗\vec{F}F.
Operații cu vectori
Pe lângă reprezentarea lor, vectorii pot fi adunați, scăzuți sau înmulțiți cu un scalar:
- Adunarea vectorilor: se face prin metoda paralelogramului sau metoda vârfului la coadă.
- Scăderea vectorilor: se face prin adunarea vectorului opus.
- Înmulțirea cu un scalar: modifică doar modulul vectorului, păstrând direcția, sau îl inversează dacă scalarul este negativ.
Exemple de vectori în viața reală
- Viteza unei mașini: are direcție și sens, nu doar valoare numerică;
- Deplasarea unui elev pe holul școlii: indică distanța și direcția parcurgerii;
- Forța vântului asupra unei corăbii: direcția și sensul vântului influențează traiectoria navei.
Importanța vectorilor
Vectorii sunt fundamentali în fizică și inginerie, deoarece majoritatea fenomenelor reale implică mărimi care nu sunt doar cantitative, ci au și direcție și sens. Înțelegerea vectorilor permite descrierea corectă a mișcării obiectelor, forțelor aplicate și interacțiunilor din natură.
Exerciții: Vectorii. Mărimi vectoriale
Exercițiul 1 – Identificarea vectorilor
Indică care dintre următoarele mărimi sunt vectoriale și care scalare (mărimi scalare):
- Viteza unei mașini
- Temperatura aerului
- Forța aplicată asupra unei uși
- Masa unui obiect
- Desplasarea unui biciclist
- Energia unui corp
Exercițiul 2 – Reprezentarea vectorială
Desenează un vector care:
- Are lungimea 5 cm și direcția spre dreapta
- Are lungimea 3 cm, orientat în sus și la stânga
Menționează modulul, direcția și sensul fiecărui vector.
Subtitlu: modifică tipul sau stilul blocului
Mută blocul Subtitlu din poziția 33 mai sus la poziția 32
Mută blocul Subtitlu din poziția 33 mai jos la poziția 34
Modifică alinierea
Modifică alinierea textului
Afișează mai multe unelte pentru blocuri
Exercițiul 3 – Operații cu vectori
Se dau doi vectori în planul cartezian:
A⃗=(3,4)\vec{A} = (3, 4)A=(3,4), B⃗=(−1,2)\vec{B} = (-1, 2)B=(−1,2)
- Calculează suma vectorilor: A⃗+B⃗\vec{A} + \vec{B}A+B
- Calculează diferența vectorilor: A⃗−B⃗\vec{A} – \vec{B}A−B
- Determină modulul vectorului A⃗\vec{A}A și B⃗\vec{B}B
Notă: Modulul unui vector V⃗=(x,y)\vec{V} = (x, y)V=(x,y) se calculează cu formula: ∣V⃗∣=x2+y2|\vec{V}| = \sqrt{x^2 + y^2}∣V∣=x2+y2
Exercițiul 4 – Vectori coliniari
Se dau trei vectori:
U⃗=(2,4)\vec{U} = (2, 4)U=(2,4), V⃗=(1,2)\vec{V} = (1, 2)V=(1,2), W⃗=(−1,−2)\vec{W} = (-1, -2)W=(−1,−2)
- Verifică dacă acești vectori sunt coliniari.
- Explică raționamentul folosit.
Exercițiul 5 – Aplicare în probleme reale
Un copil împinge un cărucior cu o forță de 50 N spre nord, iar un alt copil îl împinge cu 30 N spre est.
- Reprezintă grafic cei doi vectori.
- Determină vectorul rezultant al forțelor (mărime și direcție).
Hint: Poți folosi teorema lui Pitagora și trigonometria pentru a afla direcția: Frez=F12+F22,α=arctanF2F1F_\text{rez} = \sqrt{F_1^2 + F_2^2}, \quad \alpha = \arctan\frac{F_2}{F_1}Frez=F12+F22,α=arctanF1F2
 15.05.2025
15.05.2025